Über die Stabilität der Monde im duckschen Universum
Eine Multimedia-Veröffentlichung mit vielen YouTube-Animationen
Stefan Jordan
Astronomisches Rechen-Institut (ARI), Zentrum für Astronomie der Universität Heidelberg (ZAH), Mönchhofstr. 12--14, D-69120 Heidelberg
und Andreas Baumbach
Kirchhoff-Institut für Physik, Im Neuenheimer Feld 227, D-69120 Heidelberg
Erstveröffentlichung in "Der Donaldist 159, S. 21"
ZUSAMMENFASSUNG
Wir untersuchten die von paTrick Martin (2005) aufgestellte Hypothese, dass es in der Welt von Entenhausen drei Monde gibt, die den Heimatplaneten der Ducks in einem Abstand von jeweils 120 Grad voneinander umkreisen. Dazu benutzten wir numerische Simulationen, um zu prüfen, ob eine solche Anordnung in unserem Universum möglich wäre. Zusätzlich betrachteten wir als Alternative eine Anordnung, bei der sich zwei Monde im Abstand von jeweils 60 Grad von einem mittleren Mond befinden. Alle Konfigurationen wurden auch bezüglich ihrer Kompatibilität mit Beobachtungen in der Geschichte "Der Feuerteufel" geprüft. Tatsächlich passt keine der Simulationen wirklich zu den Hinweisen bei Barks und Fuchs, so dass wir damit einen weiteren Hinweis darauf haben, dass es im duckschen Universum ein anderes Gravitationsgesetz gibt als in unserem Universum.
Einleitung
Auf jedem der vergangenen drei D.O.N.A.L.D.-Kongresse wurde der Erstautor mehrfach darauf angesprochen, doch endlich mal den Inhalt seines Vortrages über die Stabilität der Monde im duckschen Universum auf dem Kölner Kongress am 19. März 2016 zu Papier zu bringen. Das lag außer am Inhalt sicher auch an den gezeigten Animation mit vielen unhörbaren Bums, Knalls und Rums. Endlich sind wir dieser Pflicht nun nachgekommen. Und auch die im Vortrag gezeigten Videos sind in dieser Arbeit verlinkt.
Schon 1986 hat Stefan Jordan, ebenfalls in Köln, über den Goldmond vorgetragen und die Frage diskutiert, ob in Entenhausen ein anderes Gravitationsgesetz gilt (Jordan 1986). Unter Benutzung der im Barks-Fuchs-Bericht "Verlorenes Mondgold" (Barks & Fuchs1958} gemachten Beobachtungen kam er zu dem Schluss, dass sich der Goldmond, der sich ja bekanntlich von Stella Anatium aus gesehen stets hinter dem Mond befindet, im Lagrange-Punkt L2 sein müsste. Dieser ist aber nach den Regeln der irdischen Mechanik instabil, was darauf hindeutet, dass in Entenhausen ein anderes Gravitationsgesetz gelten muss als bei uns.
Das Thema Monde in duckschen Universum wurde dann ausführlich von Martin (2005) aufgegriffen.
Wir möchten gerne in gekürzter Form auf ein paar Argumente und Schlussfolgerungen von paTrick Martin in seinem "Artikel Astronomia Nova Stellarum Anatium" eingehen.
Ein Video mit Untertiteln, in dem die einzelnen Aspekte, seines Papers zu lesen sind, findet man unter https://youtu.be/_FE5Du3BaSA (Alle Videos enthalten Untertitel die auf YouTube mit CC ein- und abschaltbar sind). Dort sind auch die Bilder aus den Barks-Fuchs-Berichten zu sehen und werden deshalb, bis auf eine Ausnahme, in dieser Arbeit nicht wiederholt.
Zunächst fiel Martin auf, dass Herr Duck völlig ohne professionelle Ausrüstung und vor allem ohne Sauerstoffmaske, aber immerhin mit Zahnbürste, auf dem Mond gelandet ist (Barks & Fuchs,1948) .
Die Expedition der Astronauten, die das düsentriebsche Röstbrot auf dem Mond entdeckte, landete dort dagegen mit Raumanzügen (Barks & Fuchs 1948).
In einer weiteren Geschichte hatte dann auch Dagobert einen Raumanzug an. Allerdings gab es in der Gegend, in der er sich befand, definitiv eine Atmosphäre, wie die in dem Bericht gezeigten Rauchzeichen beweisen (Barks & Fuchs 1948).
Als eine weitere Merkwürdigkeit beschrieb paTrick Martin außerdem den Schattenwurf Donalds, der sich auf dem Mond auf der sonnenabgewandten Seite befinden musste, weil ja die Erde als Vollerde zu sehen ist (BarksFuchs 1948).


Extrem eigenartig ist schließlich, dass auf zwei kurz aufeinander folgenden Bildern, jeweils eine gänzlich verschiedene Mondphase zu sehen ist (Barks & Fuchs1945, Bild 1a und b): zuerst ein abnehmender Mond, wie er bei uns auf der Nordhalbkugel in den Morgenstunden zu sehen ist, und kurz danach ein zunehmender Mond, der bei uns nur abends sichtbar ist.
PaTrick Martins klare Schlussfolgerung: Es gibt mehr als einen Mond.
Und zwar erstens den Mond, den Donald als Privatmann umrundet hat (MdDaPuh), zweitens den Mond mit atembarer Atmosphäre (MmaA) und schließlich unseren alten Mond (UaM). Nicht zu vergessen natürlich auch den Goldmond, auf dem der Venusianer Muchkale lebte (Barks & Fuchs1958) und dessen Bahnstabilität Jordan (1986) untersucht hat. Zu der zwielichtigen Gestalt Muchkale, die auf dem Goldmond wohnte, siehe auch Dioszeghy-Krauß et al. (2019).
Da niemals zwei der Monde gleichzeitig zu sehen sind, schloss paTrick Martin daraus, dass die drei Monde einen maximalen Abstand haben sollten, also miteinander ein gleichseitiges Dreieck bilden (Bild 4). Also haben sie zueinander einen Winkelabstand von jeweils 120 Grad. Damit erklärte paTrick auch die verschiedenen nacheinander sichtbaren Mondphasen, es sind eben zwei Monde.
Die wahrscheinlichen Eigenschaften der Monde hat paTrick in einer Tabelle zusammengefasst (Seite 42 in Martin 2005). Er vermutete, dass die drei Monde ungefähr gleich groß sein müssten.


Physikalische Voraussetzungen für unsere Simulationen
Um zu überprüfen, ob die Schlussfolgerungen von Martin (2005) in unserem Universum möglich wären, haben wir Simulationen unter Verwendung des speziell angepassten direkten N-Körpercode GPU 6 (Berczik et al. 2011, 2013) durchgeführt. Das Programm wurde in der Programmiersprache C++ geschrieben und für den effektiven Einsatz von Grafikprozessoren optimiert. Es erlaub eine sehr genaue und relativ schnelle Integration der Bahn und wird in der astronomischen Forschung verwendet.
Ein solcher Code berechnet die Bewegung von massebehafteten Körpern aufgrund ihrer Anfangspositionen und -geschwindigkeiten unter der Einwirkung ihrer gegenseitigen Gravitationskräfte. Dazu verwendet das Programm die newtonschen Gesetze und das in unserem Universum gültige Gravitationsgesetz.
Wie schon Storch (1978) gezeigt hat, gelten die in unserem Universum gültigen Gesetze der Mechanik auch in Entenhausen. Im nichtrelativistischen Grenzfall (also bei Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit und bei Anwesenheit nicht zu starker Gravitationsfelder) gelten die newtonschen Gesetze (Newton 1687).
Es gibt in Entenhausen zahllose Beispiele für die Gültigkeit des ersten newtonschen Gesetzes: Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Bewegung, sofern er nicht durch einwirkende Kräfte zur Änderung seines Zustands gezwungen wird.
Beispiele für das erste newtonsche Axiom diskutierte bereits von Storch (1978 und 1986). Hier sehen wir ein Weiteres: Donald rast in Das Bootsrennen mit einem Motorboot auf einen kleinen Wasserfall zu (Bild 2). Dann überschreitet das Boot den Punkt, an dem es den Kontakt zum Wasser verliert und daher antriebslos wird. Dennoch rast das Boot noch ein gutes Stück weiter geradeaus, bevor es dann, der Schwerkraft folgend, nach unten geflogen wäre, wenn es nicht durch einen Draht zum Stoppen gebracht worden wäre. Also erst, als eine zusätzliche Kraft durch den Draht auf das Boot ausgeübt wurde, wurde die gleichförmige Bewegung abgebremst. Offensichtlich gilt also das Trägheitsprinzip.
An der Wand von Daniel Düsentriebs Labor zeugen Schilder in "Die künstliche Kraftquelle" (Barks & Fuchs1960) davon, dass in Entenhausen auch Kraft ist gleich Masse mal Beschleunigung also das 2. newtonsche Gesetz, die Bewegung von Körpern in einem Kraftfeld beschreibt (Bild 3). Und das 3. newtonsche Gesetz Kraft gleich Gegenkraft ist implizit in dem auf dem Schild zitierten “Druck erzeugt Gegendruck” (Druck ist bekanntlich Kraft pro Fläche), den ein Panzerknacker deutlich zu spüren bekommt, enthalten. Alle drei newtonschen Gesetze gelten also im duckschen Universum.
Ob das Gravitationsgesetz allerdings in Entenhausen streng gilt, wurde, wie bereits erwähnt, schon von Jordan (1986) bezweifelt. Außerdem haben Dioszeghy-Krauß et al. (2019) Belege gefunden, dass es im Raum zwischen Stella Anatium und dem alten Mond nicht leer ist: Der Schall des am Raumschiff der Ducks vorbei rasenden Weltraumgefährts des Maharadschas ist hörbar. Unsere Berechnungen nehmen aber an, dass die Abbremsung der Himmelskörper durch eine solche Weltraumatmosphäre klein ist. Ansonsten wäre die Stabilität der Mondorbits noch geringer und auch unser alten Mond müsste auf Stella Anatium stürzen.
Simulationen der Orbits der vermuteten Monde
Konfiguration in einem Abstand von 120°
Wie können wir nun feststellen, ob eine solche dauerhafte Stellung wie in Bild 4 möglich ist? Mit unserer Simulation können wir nur prüfen, ob eine solche Anordnung in unserem Universum möglich wäre.
Dazu haben wir die beschriebene Stellung der Monde in unser Elektronengehirn am Astronomischen Rechen-Institut in Heidelberg eingefüttert und mit dem Programm GPU 6 durchgerechnet. Die Animationen wurden mit Hilfe des Programms Blackmagic Fusion 9 durchgeführt.
Die Anfangskonfiguration der Simulation der Orbits von drei Monden gleicher Masse im Abstand von 120° zeigt Bild 4.
Nach vielen Tagen Rechenzeit des Elektronengehirns spuckte unser Elektronengehirn die Ergebnisse aus. Aus diesen haben wir dann die auf https://youtu.be/jcM8PqboHIY zu sehende Animation produziert. Dabei sind die Größen und Abstände so skaliert, dass man das Ganze besser erkennen kann (Die Himmelskörper sind also viel zu groß dargestellt, in der dazugehörigen Rechnung aber nicht!).
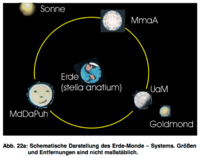
In dem Video steht die Sonne links. Stella Anatium – dargestellt wie unsere Erde in der Mitte – und die drei Monde mit gleicher Masse — gezeigt mit der Oberfläche unseres Erdmondes — werden wie Stella Anatium von links beschienen.
Tatsächlich handelt es sich bei der von paTrick vorgeschlagenen Konfiguration um eine Gleichgewichtskonfiguration, die himmelsmechanisch möglich ist. Solange die Monde ganz genau in ihrer Position bleiben, gilt das auch.
Nur was passiert, wenn die allerkleinste Störung auftritt, wie sie schon durch die Anwesenheit anderer Planeten und der Sonne unvermeidlich ist. Oder durch das Wandern von Astronauten auf diesen Himmelskörpern. Oder in unserer Berechnung durch kleinste numerische Ungenauigkeiten, die trotz des sehr präzisen Algorithmus unvermeidlich sind.
Mehre Umläufe lang bleiben die Monde in ihrer relativen Anfangsstellung von 120° zueinander. Danach geraten sie aber unvermeidlich auf andere Umlaufbahnen. Monde können herausgeschleudert werden oder, wie hier zu sehen, kollidieren. Die Kollision ist noch einmal in Zeitlupe auf https://youtu.be/vK9HyL_luSo zu sehen.
In unserem Universum wäre eine solche Stellung der Monde also nicht stabil und würde zur schnellen Auflösung oder Zerstörung des Systems führen. In unserer Simulation dauerte dieser Vorgang 27 Monate (Umläufe der Monde).

Monde in den Lagrange-Punkten
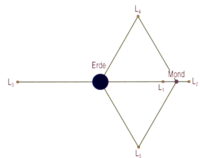
Tatsächlich gibt es die Möglichkeit, drei Monde unter Annahme der Verhältnisse in unserem Universum auf eine gemeinsame stabile Umlaufbahn zu bringen, und zwar wenn sich zwei von ihnen in der Nähe der sogenannten Lagrangepunkte L4 und L5 (siehe Bild 6 und 7) aufhalten. Allerdings wären die beiden Extra-Monde dann in einem Abstand von nur 60°.
Für den Goldmond kommt nur der Lagrangepunkt L2 in Frage, der sich hinter dem Alten Mond (UaM) befindet. Für die ersten Simulationen haben wir den Goldmond weggelassen.
Und selbst in den Lagrangepunkten L4 und L5 funktioniert eine stabile Konfiguration nur unter bestimmten Voraussetzungen.
Haben nämlich alle drei Monde eine vergleichbar große Masse (Bild 8), ist die Konfiguration ebenfalls instabil, wie die Animation auf https://youtu.be/Ha4pYP35RaM zeigt, bei der wir angenommen haben, dass alle Massen exakt gleich sind.


Tatsächlich sind die Lagrangepunkte L4 und L5 nur stabil, wenn die beiden dort befindlichen Monde eine Masse haben, die kleiner ist als ein 24.96tel der Masse des mittleren Mondes, bei uns wäre das UaM. In dieser Animation habe wir das Massenverhältnis auf 1:30 gesetzt. Und diese Situation ist sehr stabil. Selbst deutliche Abweichungen der Monde von ihrer Ursprungsposition ließen sie wieder zurückschwingen. Dieses Verhalten ist genau das, was man mit Stabilität bezeichnet.
Die Animation dieser Konfiguration kann auf https://youtu.be/Fy5Gc-vOUow (Bild 9) betrachtet werden. Das Video zeigt 33 Monate stabiler Bewegung. Diese würde aber auch darüber hinaus beliebig lange andauern.
Sollten die Monde den gleichen Durchmesser haben wie der mittlere Mond, müsste die Dichte der anderen Monde mindestens 25 mal geringer sein als bei unserem alten Mond. Ungewöhnlich, aber ungewöhnliche Dinge sind ja manchmal gewöhnlich in Entenhausen.
Auf jeden Fall ist es eigenartig, wenn ausgerechnet der Mond MdDaPuh mit nur einem 30stel oder 25stel der Mondmasse eine Atmosphäre halten könnte, wie in Barks & Fuchs (1948) beschrieben. Das wäre nur möglich, wenn der Radius 900 mal bzw. 625 mal kleiner wäre. Dem widersprechen aber die Bilder in Barks & Fuchs (1945), die eine von Entenhausen aus gesehen vergleichbare Größe vermuten lassen (in Bild 1 sieht man einen Größenunterschied von einem Faktor 2, wenn man von einem gleichen Gesichtsfeld des Bildes ausgeht).
In einer weiteren Simulation fügen wir jetzt noch den Goldmond im Lagrangepunkt L2 hinzu (Bild 10). Dieser würde allerdings nach wenigen Monaten weit heraus geschleudert werden und damit auf eine andere Umlaufbahn gelangen, wie die Simulation auf https://youtu.be/Yl3g4Cq5LyE zeigt.

Die Mondphasen
Nach der Untersuchung der Stabilität wollen wir auch noch überprüfen, ob die von Martin (2005) vorgeschlagene Anordnung der Monde in 120° Winkelabstand die gleichzeitige Sichtbarkeit der beiden Mondphasen in Bild 1 erklären kann.
Diese Animationen konnten aus Zeitgründen nicht in Stefan Jordans Vortrag in Köln gezeigt werden.
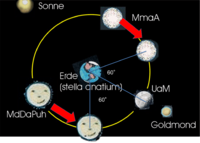
Als erstes wurde wieder die Konfiguration getestet, bei der die Monde sich in einem Abstand von 120° befinden. Bild 11 und das dazu gehörige Video https://youtu.be/k_UCsuC0c38 zeigen zwar in einem kurzen Augenblick gleichzeitig einen abnehmenden und einen zunehmenden Mond. Allerdings sind die Sicheln deutlich schmaler als in den von Barks übermittelten Bildern.
Alle anderen Simulationen, bei denen der Abstand vom mittleren Mond UaM nur 60° beträgt, zeigen zu keinem Zeitpunkt eine mit den Beobachtungen von Barks kompatible Situation.


Schlussfolgerung
Die verschiedenen Barks-Berichte beschreiben sehr unterschiedliche Eigenschaften der Monde. Eine Erklärung dafür könnte sein, dass es, wie Martin (2005) vermutet, im duckschen Universum in Wirklichkeit drei große Monde gibt. Da es im Werk von Barks kein einziges Bild gibt, auf dem die Monde in Entenhausen dicht beieinander stehen, liegt es nahe, dass die relativen Abstände ca. 120 Grad betragen.
Allerdings ist auch diese Konfiguration nicht mit den Beobachtungen der Mondphasen kompatibel, es sei denn, wir erlauben uns die Vermutung, dass Carl Barks nicht besonders exakt gezeichnet hat.
Wir haben mit numerischen Simulationen gezeigt (und dies entspricht auch den analytisch zu erwartenden Ergebnissen), dass drei Monde im Abstand von 120° auf der gleichen Umlaufbahn (und die ist ja durch die Umlaufzeit nach dem 3. keplerschen Gesetz vorgegeben) keine stabile Konfiguration darstellen. In der unten stehenden Tabelle haben wir die Ergebnisse der Simulationen zusammengefasst.
Als einzige stabile Lösung haben wir gefunden, dass sich zwei der Monde im Abstand von jeweils 60° vom mittleren Mond befinden können, aber eine im Vergleich zu UaM extrem geringe Masse besitzen müssten. Ein so geringer Abstand ist aber wegen der fehlenden Beobachtungen eines solchen Konfiguration in Entenhausen sehr unwahrscheinlich.
Wenn die Vermutung dreier Monde um den Heimatplaneten der Ducks von Martin (2005) korrekt ist, müsste in Entenhausen in der Tat ein anderes Gravitationsgesetz gelten, wie schon von Jordan (1986) vermutet.
Die Konsequenz dessen wäre, dass sich Entenhausen nicht vollständig in unserem Universum befinden kann.
| Abstand der Monde | MasseMdDaPuh/MasseUaM | Masse MmaA/MasseUaM | Goldmond | stabil? | erklärt Mondphasen? |
|---|---|---|---|---|---|
| 120° | 1 | 1 | nein | nein | große Abweichung |
| 60° | 1 | 1 | nein | nein | nein |
| 60° | 1/30 | 1/30 | nein | ja | nein |
| 60° | 1/30 | 1/30 | ja | Goldmond instabil | nein |
Literatur
Barks, C., Fuchs, E. 1945, Der Feuerteufel, FC108/2, TGDD 89, BL-DO 4
Barks, C., Fuchs, E. 1948, Wettrennen zum Mond, WDC93, MM 36/48, TGDD 22, B-LWDC 13
Barks, C., Fuchs, E. 1958, Verlorenes Mondgold, US24/1, MM 15-16/75, TGDD 114, BL-OD 15
Barks, C., Fuchs, E. 1960, Die künstliche Kraftquelle, FC 1184/4, MM 7/62, TGDD 143, BL-DÜ 5
Barks, C., Fuchs, E. 1961, Das Bootsrennen, WDC 255/1, MM 45/83, TGDD 33, BL-WDC 44
Barks, C., Fuchs, E. 1961, Der Volltreffer, US37/3, MM 4/63, BL-DÜ 6
Barks, C., Fuchs, E. 1963, Der Lockruf des Mondgoldes, US49/1, MM 22-23/65, BL-OD 27
Martin, p. 2005, Astronomia Nova Stellarum Anatium, Der Donaldist 125, 38
Newton, I. 1687, Philosophiae Naturalis Principia Mathematica
Storch, H. 1978, Klima in Entenhausen, Der Hamburger Donaldist 13, 10
Storch, H. 1986, Anatidische Physik, Der Donaldist 55, 3
Zupfer, K. Z. 1998, Geodäsie an der Gumpe, Der Donaldist, 101, 24
